Question

NO LINKS!! Use tests for symmetry to determine which graphs from the list below are symmetric with respect to the y-axis, the x-axis, and the origin. (Select all that apply.) Part 2​

Answer 1

`y=-(1)/(5)x^3`

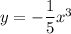
Explanation:

A graph is symmetric with respect to the origin if it is unchanged when reflected across both the x-axis and y-axis.

Linear functions are symmetric with respect to the origin if they are proportional.

Quadratic functions are not symmetric with respect to the origin. They are symmetric with respect to one axis if that axis is their axis of symmetry.

Cubic functions are symmetric about the origin if their point of inflection is the origin.

Square root functions are not symmetric about the origin.

There are no proportional linear functions in the given answer options.

There are two cubic functions in the given answer options.

Test to see if they are symmetric with respect to the origin.

Test for symmetry

If a function is symmetrical about the origin, when y is replaced with (-y) and x is replaced with (-x), the resulting function will be equal to the original function.

Given function:

`y=-(1)/(5)x^3`

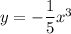
Replace y with (-y) and x with (-x):

`\implies -y=-(1)/(5)(-x)^3`

`\implies -y=(1)/(5)x^3`

`\implies y=-(1)/(5)x^3`

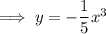
Therefore, as the function is equal to the original function, this function is symmetric with respect to the origin.

Given function:

`y=x^3-9`

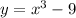
Replace y with (-y) and x with (-x):

`\implies -y=(-x)^3-9`

`\implies -y=-x^3-9`

`\implies y=x^3+9`

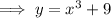
Therefore, as the function is not equal to the original function, this function is not symmetric with respect to the origin.