Question

A disk of radius 10 cm speeds up from rest. it turns 60 radians reaching an angular velocity of 15 rad/s. what was the angular acceleration?

b. how long did it take the disk to reach this velocity?​

Answer 1

a) The angular acceleration is 1.875 radians per square second.

b) The time taken by the disk to reach the final angular speed is 8 seconds.

Step-by-step explanation:

a) Let suppose that the disk accelerates uniformly, given that initial and final angular speed (
`\omega_(o)`,
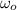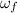`\omega_(f)`), in radians per second, and change in angular position (
`\Delta \theta`), in radians, are known. The angular acceleration (
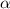`\alpha`), in radians per square second, are found by using this expression:

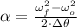`\alpha = (\omega_(f)^(2)-\omega_(o)^(2))/(2\cdot \Delta \theta)` (1)

If we know that
`\omega_(o) = 0\,(rad)/(s)`,
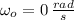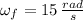`\omega_(f) = 15\,(rad)/(s)` and
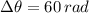`\Delta \theta = 60\,rad`, then the angular acceleration of the disk is:

`\alpha = (\omega_(f)^(2)-\omega_(o)^(2))/(2\cdot \Delta \theta)`

`\alpha = 1.875\,(rad)/(s^(2))`

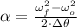
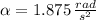
The angular acceleration is 1.875 radians per square second.

b) The time taken by the disk to reach the final angular velocity is determined by the following kinematic formula:

`t = (\omega_(f)-\omega_(o))/(\alpha)` (2)

Where
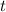`t` is the time, in seconds.

If we know that
`\omega_(o) = 0\,(rad)/(s)`,
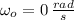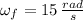`\omega_(f) = 15\,(rad)/(s)` and
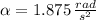`\alpha = 1.875\,(rad)/(s^(2))`, then the time taken by the disk is:

`t = (\omega_(f)-\omega_(o))/(\alpha)`

`t = 8\,s`

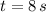
The time taken by the disk to reach the final angular speed is 8 seconds.