Quadratic formula
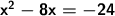
We move the expression to the left side and then change its sign.
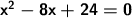
We use the quadratic formula to solve the quadratic equation ax^2 + bx + c = 0
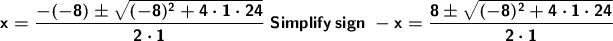
A negative number raised to the power of an even number is a positive number. So the negative sign is removed.

We organize the part that can be taken from the radical sign inside the square root.

We reduce the fraction.
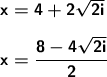
We reduce the fraction.
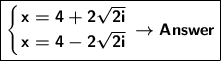
We change only the address: x=4+2i√2 or x=4-2-2i√2. LAST ALTERNATIVE