keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the equation above
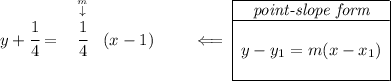
so we're really looking for the equation of a line whose slope is 1/4 and that it passes through (-10 , -3)
standard form for a linear equation means
• all coefficients must be integers, no fractions
• only the constant on the right-hand-side
• all variables on the left-hand-side, sorted
• "x" must not have a negative coefficient

