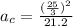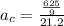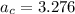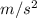Answer:
The centripetal acceleration of the car is
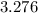
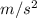 .
.
Step-by-step explanation:
Centripetal Acceleration Equation
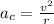
Lets convert
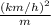 to
to
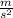
First convert km/h to m/s. We can use the following relationships.
1 km = 1000 m
1 hour = 60 min
1 min = 60 sec
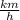 to
to
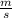
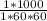 simplifies to
simplifies to
 .
.
Now we have
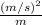
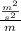
Multiply the numerator by the reciprocal of the denominator.
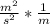
Combine.
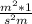
Factor
 out of
out of
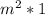 .
.
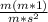
Cancel the common factor.
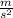
Multiply the speed value in km/h by
 to get the speed value in m/s.
to get the speed value in m/s.