Question

If P(x,6) and Q(14,-2) are two points and distance between them in 10 units, find the possible values of x.

Answer 1

x = 8 , x = 20

Explanation:

Calculate PQ using the distance formula and equate to 10

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

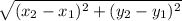
with (x₁, y₁ ) = Q (14, - 2 ) and (x₂, y₂ ) = P (x, 6 )

PQ =
`√(x-14)^2+(6-(-2))^2)`

=
`√((x-14)^2+(6+2)^2)`

=
`√((x-14)^2+8^2)`

=
`√((x-14)^2+64)`

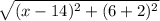
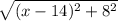
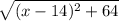
Equating to 10

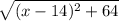`√((x-14)^2+64)` = 10 ( square both sides to clear the radical )

(x - 14)² + 64 = 10² = 100 ( subtract 64 from both sides )

(x - 14)² = 36 ( take square root of both sides )

x - 14 = ±
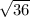`√(36)` = ± 6 ( add 14 to both sides )

x = 14 ± 6

then

x = 14 - 6 = 8 or x = 14 + 6 = 20