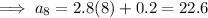Question

In an Arithmetic Progression (AP), the first

term is 3, and the sum of the first and the sixth
terms is 20. What is the 8th term

Answer 1

The 8th term of the AP= 113/5 or 22.6

Answer 2

22.6

Explanation:

Given:

• a = 3

• a + a₆ = 20

Find the value of a₆:

`\implies a+a_6=20`

`\implies a_6=20-a`

`\implies a_6=20-3`

`\implies a_6=17`

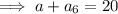
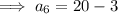
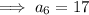
Therefore:

• a = 3

• a₆ = 17

General form of an arithmetic sequence:

`\boxed{a_n=a+(n-1)d}`

Where:

• 
  `a_n` is the nth term.
• a is the first term.
• d is the common difference between terms.
• n is the position of the term.

Substitute a = 3 and a₆ = 17 into the formula and solve for d:

`\begin{aligned}\implies a_6=3+(6-1)d&=17\\3+5d&=17\\5d&=14\\d&=2.8\end{aligned}`

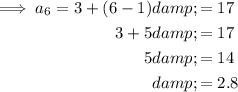
Therefore, the equation for the nth term is:

`\implies a_n=3+(n-1)2.8`

`\implies a_n=3+2.8n-2.8`

`\implies a_n=2.8n+0.2`

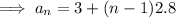
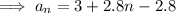
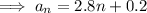
To find the 8th term, substitute n = 8 into the equation for the nth term:

`\implies a_8=2.8(8)+0.2=22.6`