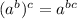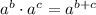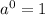Answer:
Proof below.
Explanation:
General form of a geometric sequence:
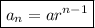
Where:
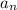 is the nth term.
is the nth term.- a is the first term.
- r is the common ratio.
- n is the position of the term.
If the pth, qth, rth terms of the geometric progression are a, b, c respectively, then:
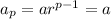
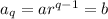
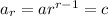
Substitute the expressions for a, b and c into the LHS of the given equation and solve:
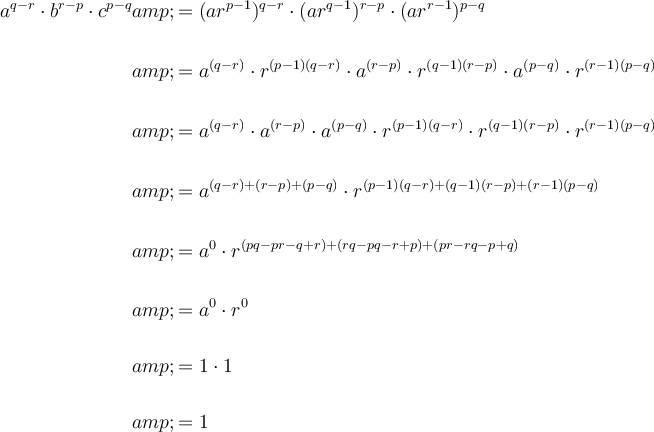
Hence proving that:
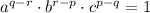
------------------------------------------------------------------------
Exponent rules used: