Question

After a 20% discount, you purchase a television for $240. What was the television's

price before the reduction? (Define a variable, create an equation, solve using algebra,
and answer in a sentence.)

Answer 1

The original price of the television before the 20% discount was applied, is $300

Explanation:

Applying a Discount

Whenever you decrease a value by a certain percentage, let's say "x"%, all you're doing is calculating (100 - x)% of the item. So in this case when a 20% discount is applied, the value is decreasing by 20%, and the new value is (100-20) or 80% it's original value.

Defining an Equation

So we have one unknown we are solving for, which is the original price before reduction, and let's just represent this with: "P". After applying a 20% discount by calculating 80% the value, we get the value 240.

To calculate 80% of a value, you simply multiply it by the decimal form, which is calculated by dividing a percentage by 100, so 80% = 0.80

So we can derive the following equation:
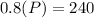`0.8(P) = 240` and from here it's just one step to solve this equation... divide by 0.80 to isolate the "P" which gets us:
`P = (240)/(0.8) = 300`

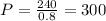
The original price of the television before the 20% discount was applied, is $300