Question

Given f(x)=5√x+3-2, which graph best represents f⁻¹(x) ?

You may use the graphing calculator.
Desmos Graphing Calculator
Source hetps:/munu desmos comvalculator

Answer 1

graph A

Explanation:

Using Desmos

If you use a graphing calculator to solve this you just swap the x and y so:

`y=5√(x+3)-2\implies x=5√(y+3)-2` and then choose whichever aligns with the graph most accurately (graph A). I attached an image using desmos.

Solving it Algebraically

If you want to solve for y, you first add 2

`x+2=5√(y+3)`

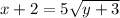
divide both sides by 5

`(x+2)/(5)=√(y+3)`

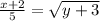
square both sides

`((x+2)/(5))^2=y+3`

subtract 3 from both sides

`((x+2)/(5))^2-3=y`

distributing the exponent we get:

`(((x+2)^2)/(25))-3=y`

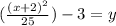
move the 1/25 infront

`(1)/(25)(x+2)^2-3=y`

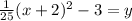
we actually have the vertex since it's in vertex form (-2, -3) and you may be asking why this is important, well in an inverse function the domain and range are swapped, and in original function it had a range of y values greater than or equal to -2, so this is the domain of the new function... this conveniently happens at the vertex where this function goes from decreasing to increasing and continues to increase on the rest of the domain. This means the inverse function is increasing for all values of x and only graph A has this property, so it's the only plausible answer