Question

If a₁+a₂=1, a₂+a₃=2, a₃+a₄=3, a₄+a₅=4,....a₅₀+a₅₁=50 and a₅₁+a₁=51, then what is the sum of a₁, a₂, a₃,....., a₅₁ ?

A. 663
B. 1326
C. 1076
D. 538
E. 665

Answer 1

Answer: Choice A) 663

=========================================================

Step-by-step explanation:

Notice that each term
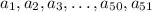`a_1, a_2, a_3, \ldots, a_(50), a_(51)` appears exactly twice in all of the sums mentioned

a₁+a₂=1, a₂+a₃=2, a₃+a₄=3, a₄+a₅=4,....a₅₀+a₅₁=50 and a₅₁+a₁=51

What we can do is add up the left hand sides of those sums, separate from the right hand sides

L = sum of the left hand sides

`L = (a_1+a_2)+(a_2+a_3)+\ldots+(a_(50)+a_(51))+(a_(51)+a_(1))\\\\L = 2(a_1+a_2+\ldots+a_(50)+a_(51))`

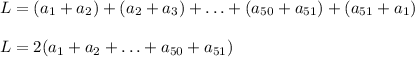
R = sum of the right hand sides

`R = 1+2+3+\ldots+50+51\\\\\displaystyle R = (51/2)*(1+51)\\\\\displaystyle R = 1326\\\\`

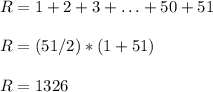
To compute the value of R, I used the formula
`1+2+3+\ldots+n = (n/2)*(1+n)`

-----------------------------

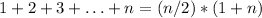
After establishing L and R, we equate the items and divide both sides by two like so:

`L = R\\\\2(a_1+a_2+\ldots+a_(50)+a_(51)) = 1326\\\\a_1+a_2+\ldots+a_(50)+a_(51) = 1326/2\\\\a_1+a_2+\ldots+a_(50)+a_(51) = \boldsymbol{663}\\\\`

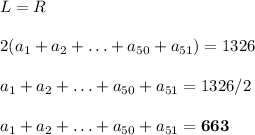
This points us to choice A as the final answer.