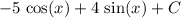Answer:
(i):
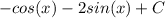
(ii):
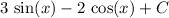
(iii):
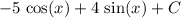
Explanation:
Indefinite Integral Properties
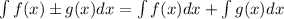
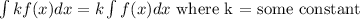
Solving the Integral Problems
(i)
original expression
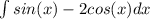
rewrite the expression using the addition/subtraction property
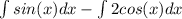
Now from here we can move the constant in front to get:
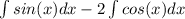
from here we can use our knowledge of derivatives to integrate this expression.
![(d)/(dx)[cos(x)] = -sin(x)\\(d)/(dx)[sin(x)] = cos(x)](https://img.qammunity.org/2023/formulas/mathematics/college/u3okflsycxfi5k647o5mursgnscilow9av.png)
similarly to our indefinite integral properties, whenever we have a constant, we can move it in front and differentiate the problem, so that means that:
![(d)/(dx)[-cos(x)]=-(d)/(dx)[cos(x)]=-[-cos(x)]=sin(x)](https://img.qammunity.org/2023/formulas/mathematics/college/9vrr4guiwklisw130ua3d37m1h6i88lwc0.png) , so the indefinite integral of sin(x) is -cos(x), not just cos(x). For cos(x) it's just sin(x). This gives us the expression:
, so the indefinite integral of sin(x) is -cos(x), not just cos(x). For cos(x) it's just sin(x). This gives us the expression:
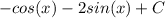
always make sure to add the "C" value which is some constant, since whenever we differentiate, this constant will become zero,
(ii)
This problem is essentially using the same properties, so we start off with
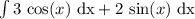
now from here we rewrite using our identities
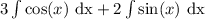
now from here we integrate using our knowledge of derivatives
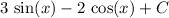
(iii)
Original Expression:
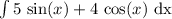
from here rewrite using integral properties

from here we can integrate easily: