Answer:
1. Refer to the explanation below.
2. y = 20
3. x = 16
4. 16 students bought a cup of orange juice and 20 students bought a sandwich. Both values are correct (refer to work below).
Step-by-step explanation:
To solve the given problem involving a system of linear equations, we can use the method of elimination to find the number of students who bought orange juice (represented as 'x') and the number of students who bought a sandwich (represented as 'y').
Given system of equations:


1. What should you do to eliminate one of the variables.

To "eliminate" one of the variables, we can manipulate the equations to have coefficients that are opposites for one of the variables and then add or subtract the equations from each other.
Equation (1) and (2) have a varible 'x' with the same coefficient of "1." We can simply subtract equation (2) from equation (1). This will eliminate the varible 'x,' making an easy equation to solve for 'y'. We will see how this works below.

2. Finding the value of 'y'.

We have,

Subtracting the equations gives us:
![\Longrightarrow [x+3y=76]-[x+y=36]\\\\\\\\\Longrightarrow (x-x)+(3y-y)=(76-36)\\\\\\\\\Longrightarrow 2y=40](https://img.qammunity.org/2023/formulas/mathematics/high-school/k4mstzi1o7v1a8945sr2l1oatohc1fr4tw.png)
Dividing by 2 gives us the value of 'y':
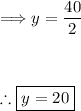
Thus, the value of 'y' is 20.

3. Finding the value of 'x'.

Now that we have the value for 'y', we can substitute it back into one of the original equations to find 'x'. Using equation (2):
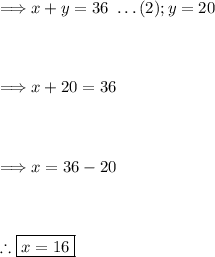
Thus, the value of 'x' is 16.

4. Interpreting the solution and checking the solution.

The solution can be interpreted as follows: 16 students bought a cup of orange juice, and 20 students bought a sandwich.
To check the solution, we substitute the values of 'x' and 'y' into both original equations:
Equation (1):
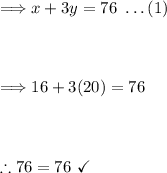
Equation (2):
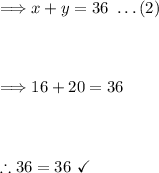
The check confirms that our values of x = 16 and y = 20 are correct. Thus, our solution meets the criteria given in the problem.