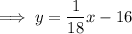Answer:

Explanation:

Given points:
- Let (x₁, y₁) = (0, -16)
- Let (x₂, y₂) = (18, -15)
Substitute the given points into the slope formula to find the slope of the line:
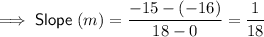

The y-intercept is the value of y when x = 0.
Therefore, from the given point (0, -16), the y-intercept of the line is -16.
Finally, substitute the found slope and y-intercept into the formula: