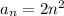Question

Find the nth term of this quadratic sequence
2, 8, 18, 32, 50,

Answer 1

`a_n=2n^2`

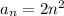
Explanation:

Given sequence:

• 2, 8, 18, 32, 50, ...

Work out the differences between the terms until the differences are the same:

`2 \underset{+6}{\longrightarrow} 8 \underset{+10}{\longrightarrow} 18 \underset{+14}{\longrightarrow} 32 \underset{+18}{\longrightarrow} 50`

`6 \underset{+4}{\longrightarrow} 10 \underset{+4}{\longrightarrow} 14\underset{+4}{\longrightarrow} 18`

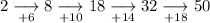
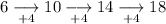
As the second differences are the same, the sequence is quadratic and will contain an n² term.

The coefficient of n² is always half of the second difference.

Therefore, the coefficient of n² is 2 (since 4 ÷ 2 = 2).

To work out the nth term of the sequence, write out the numbers in the sequence 2n² and compare this sequence with the sequence given in the question.

`\begin{array}c\cline{1-6} n & 1 & 2 & 3 & 4 & 5\\\cline{1-6} 2n^2 & 2 & 8&18&32&50\\\cline{1-6} \sf operation&&&&&\\\cline{1-6} \sf sequence&2&8&18&32&50\\\cline{1-6} \end{array}`

Therefore, there is no needed additional operation, and so the nth term is:

`a_n=2n^2`

Answer 2

• t(n) = 2n²

-------------------------

Let the expression for the nth term be:

• t(n) = an² + bn + c, where a, b, c are constants

We have:

• t(1) = 2, t(2) = 8, t(3) = 18, t(4) = 32, t(5) = 50, ...

Substitute n:

• t(1) = a(1²) + b(1) + c = a + b + c = 2
• t(2) = a(2²) + b(2) + c = 4a + 2b + c = 8
• t(3) = a(3²) + b(3) + c = 9a + 3b + c = 18

The difference of the first two and the second two equations:

• 4a - a + 2b - b + c - c = 8 - 2 ⇒ 3a + b = 6
• 9a - 4a + 3b - 2b + c - c = 18 - 8 ⇒ 5a + b = 10

From the two last equations we get the value of a:

• 5a - 3a = 10 - 6 ⇒ 2a = 4 ⇒ a = 2,

Find b:

• 3*2 + b = 6 ⇒ 6 + b = 6 ⇒ b = 0

Find c:

• 2 + 0 + c = 2 ⇒ c = 0

The nth term is:

• t(n) = 2n²