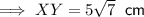Question

If XY is a chord of a circle with centre O and P is a point on XY such that YP = 4PX, OP = 6cm and the radius of the circle is 8cm, find the length of the chord XY.

Answer 1

`XY=5√(7)\;\; \sf cm`

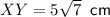
Explanation:

If YP = 4PX then the ratio of XP : PY = 1 : 4.

Let XP = x and PY = 4x, therefore the length of XY = 5x.

Let M be the midpoint of chord XY.

Therefore, if XY = 5x then XM = MY = 2.5x.

So PM = 1.5x.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Use Pythagoras Theorem to create two expressions for OM².

For right triangle OMP:

• a = MP = 1.5x
• b = OM
• c = OP = 6

`\implies MP^2+OM^2=OP^2`

`\implies (1.5x)^2+OM^2=6^2`

`\implies 2.25x^2+OM^2=36`

`\implies OM^2=36-2.25x^2`

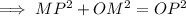
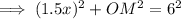
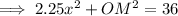
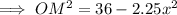
For right triangle OMY:

• a = MY = 2.5x
• b = OM
• c = OY = 8

`\implies MY^2+OM^2=OY^2`

`\implies (2.5x)^2+OM^2=8^2`

`\implies 6.25x^2+OM^2=64`

`\implies OM^2=64-6.25x^2`

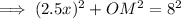
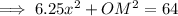
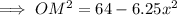
Use the method of substitution to solve for x:

`\implies OM^2=OM^2`

`\implies 36-2.25x^2=64-6.25x^2`

`\implies 4x^2=28`

`\implies x^2=7`

`\implies x=√(7)`

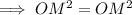
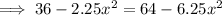
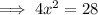
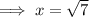
As XY = 5x, then:

`\implies XY=5√(7)\;\; \sf cm`