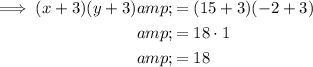Question

Given that x+y=13, xy=-30 and x>y, find the values of ( x+3)(y+3)

Answer 1

x = 15 and y = -2

(x + 3)(y + 3) = 18

Explanation:

Given equations:

`\begin{cases}x+y=13\\xy=-30\end{cases}`

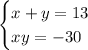
Rewrite the first equation to make y the subject:

`\implies y=13-x`

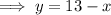
Substitute the found expression for y into the second equation and solve for x:

`\begin{aligned}xy&=-30\\y=13-x \implies x(13-x)&=-30\\13x-x^2&=-30\\-x^2+13x+30&=0\\x^2-13x-30&=0\\x^2+2x-15x-30&=0\\x(x+2)-15(x+2)&=0\\(x-15)(x+2)&=0\\\\\implies x-15&=0 \implies x=15\\\implies x+2&=0 \implies x=-2\end{aligned}`

`\textsf{When}\;x=15 \implies y=-2`

`\textsf{When}\;x=-2 \implies y=15`

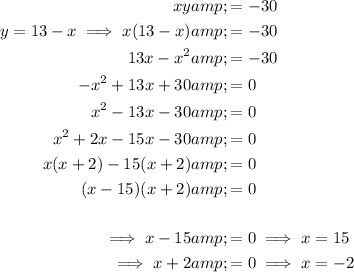
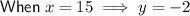
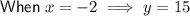
As x > y then:

• x = 15
• y = -2

Substitute the found values of x and y into the equation:

`\begin{aligned}\implies (x+3)(y+3)&=(15+3)(-2+3)\\&=18 \cdot 1\\&=18\end{aligned}`

Answer 2

• 18

-----------------------------

Given

• x + y = 13,
• xy = -30 and
• x > y

Find the value of (x + 3)(y + 3)

Distribute and regroup:

• (x + 3)(y + 3) =
• xy + 3x + 3y + 9 =
• xy + 3(x + y) + 9

Substitute values:

• - 30 + 3(13) + 9 =
• - 30 + 39 + 9 =
• 18