Answer:
ΔNOP is obtuse triangle and isosceles triangle.
Explanation:
An acute triangle has three angles that each measure less than 90°.
An obtuse triangle is a triangle with one angle greater than 90°.
A right triangle is a triangle with one 90° angle represented by the symbol ∟.
From inspection of the triangle, it appears that angle P is greater than 90°, which means it is an obtuse triangle.
This can be confirmed by using the cosine rule to calculate angle P.

Therefore:
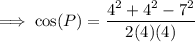
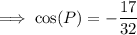
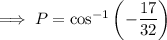
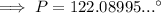
As 122.1° > 90°, this proves that triangle NOP is obtuse.
An equilateral triangle has three sides of equal length.
A scalene triangle has three sides of differing lengths.
An isosceles triangle has two sides of equal length.
Therefore, as NP = OP ≠ ON, the triangle has two sides of equal length and so it an isosceles triangle.