Answer:
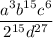
Explanation:
Given expression:
![\left[(2^(-3)ab^0(c^(-2)d^3)^(-2))/(2^2a^0(b^5c^(-2))^(-1)d^3) \right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/f379iw2gd45jr8i3ld2bwt9g1vq9rpulj2.png)
Following the order of operations, begin by applying exponent rules to the parentheses in the numerator and denominator.

![\implies \left[(2^(-3)ab^0c^((-2 \cdot -2))d^((3 \cdot -2)))/(2^2a^0b^((5 \cdot -1))c^((-2 \cdot -1))d^3) \right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/yz6cmin8m53c1iahkso2ta0lqzf44b71tx.png)
![\implies \left[(2^(-3)ab^0c^(4)d^(-6))/(2^2a^0b^(-5)c^(2)d^3) \right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/azsiv1sdikkur0cmgc3gmyiqglo23x63o0.png)
Notice there are two terms with a zero exponent.
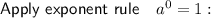
![\implies \left[(2^(-3)a(1)c^(4)d^(-6))/(2^2(1)b^(-5)c^(2)d^3) \right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/2dsper9c50rfuojlf3sp1slv5g95ifpky0.png)
![\implies \left[(2^(-3)ac^(4)d^(-6))/(2^2b^(-5)c^(2)d^3) \right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/rc4q7ikxez80ayu7tekbwld4t5y9j6ueoc.png)
Separate the terms:
![\implies \left[(2^(-3))/(2^2) \cdot (a)/(b^(-5)) \cdot (c^(4))/(c^(2)) \cdot (d^(-6))/(d^3) \right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/w76wj4lyg8c12ibl4k8otgneqgp2ywammy.png)

![\implies \left[2^((-3-2)) \cdot (a)/(b^(-5)) \cdot c^((4-2)) \cdot d^((-6-3))\right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/duyvleupc1jg3kodlb5cq3wte7br9epdxf.png)
![\implies \left[2^(-5) \cdot (a)/(b^(-5)) \cdot c^(2) \cdot d^(-9)\right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/71cu1ei5x8msz05fqp5z8yu1so3cfmcp93.png)

![\implies \left[2^(-5) \cdot a \cdot b^(5) \cdot c^(2) \cdot d^(-9)\right]^3](https://img.qammunity.org/2023/formulas/mathematics/high-school/9zsfldau0fgr5k8immk5fn1ispb02pu1w5.png)

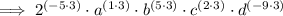
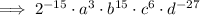
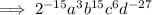
To give the expression as a rational with positive exponents,

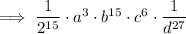
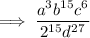
Note: I have left 2¹⁵ as an exponent with base 2. As 2¹⁵ = 32768, you can substitute 2¹⁵ for 32768 in the final answer, if you so wish.