Answer:
3y
Explanation:


Given dimensions of the cylinder:
Therefore, the equation for the volume of the cylinder is:

Given dimensions of the cone:
- diameter of base = 2x ⇒ r = x
- h = ?
Therefore, the equation for the volume of the cone is:
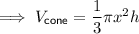
As the cylinder and the cone have the same volume, substitute the equation for the volume of the cylinder into the equation for the volume of the cone an solve for h:
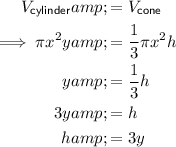
Therefore, the height of the cone is 3y.