Question

Actice Problems
Graph y>x² + 2x + 1.
y ≥ −x² + 4x + 1

Answer 1

Check the picture below.

so, we really graph the EQUATION of the expression, in this case we'd graph then h y = x² + 2x + 1. and y = −x² + 4x + 1.

then we notice that on the equation of the left-hand-side, it has "y>", meaning that "y is greater than", but never equals to that parabola, so, the line is dashed, meaning the border of the parabola is not part of the shaded area, or TRUE region.

for the one on the right-hand-side, we have "y⩾" or "y is greater than or equals", so the line is a solid line, pointing out the border of that parabola is included in the shaded part or TRUE region.

to check what section is true or not true, well, we can always pick a point on either side and check, so for example hmmmm let's check for the left-hand-side, hmmm the point above the parabola say hmmmm (2 , 3), so x = 3 whilst y = 3

`3 > (2)^2+2(2)+1\implies 3 > 4+4+1\implies 3 > 9\leftarrow \textit{is this true?}`

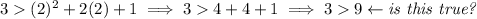
is 3 really greater than 9? well hell nope, so that's "false", so that region is the false region, thus is not shaded, that way we know the other region is the "true" region, and so that's the one we shade.