Answer:
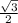 sinx -
sinx -
 cosx
cosx
Explanation:
using the sum identity for cosine
cos(a + b) = cosacosb - sinasinb
then
cos(x +
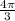 )
)
= cosxcos(
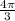 ) - sinxsin(
) - sinxsin(
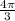 )
)
[
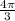 is an angle in the third quadrant where sin and cosine < 0 ]
is an angle in the third quadrant where sin and cosine < 0 ]
[ the related acute angle to
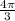 =
=
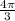 - π =
- π =
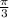 ]
]
= cosx × - cos(
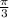 ) - sinx × - sin(
) - sinx × - sin(
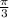 )
)
= cosx × -
 - sinx × -
- sinx × -
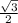
= -
 cosx +
cosx +
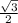 sinx
sinx
=
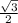 sinx -
sinx -
 cosx
cosx