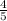Question

Find all values of m for which the equation has one real solution.
(m + 1)t² + 5 = -6t

Answer 1

m =
`(4)/(5)`

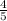
Explanation:

given a quadratic equation in standard form

ax² + bx + c = 0 ( a ≠ 0 )

then the nature of the roots can be found using the discriminant

Δ = b² - 4ac

• if b² - 4ac > 0 then roots are real and irrational

• if b² - 4ac = 0 then the roots are real and equal

• if b² - 4ac < 0 then roots are not real

For

(m + 1)t² + 5 = - 6t ( add 6t to both sides )

(m + 1)t² + 6t + 5 = 0 ← in standard form

with a = m + 1 , b = 6 , c = 5

for the equation to have only one solution then

b² - 4ac = 0

6² - 4 × (m + 1) × 5 = 0

36 - 20(m + 1) = 0 ( subtract 36 from both sides )

- 20(m + 1) = - 36 ( divide both sides by - 20 )

m + 1 =
`(-36)/(-20)` =
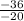`(9)/(5)` ( subtract 1 from both sides )

m =
`(4)/(5)`