Question

The graph of f(x) |x] is reflected across the y-axis and

translated to the left 5 units. Which statement about the
domain and range of each function is correct?

A. Both the domain and range of the transformed
function are the same as those of the parent function.

B. Neither the domain nor the range of the transformed
function are the same as those of the parent function.

C. The range of the transformed function is the same as
the parent function, but the domains of the functions
are different.

D. The domain of the transformed function is the same
as the parent function, but the ranges of the functions
are different.

Answer 1

A. Both the domain and range of the transformed function are the same as those of the parent function.

Explanation:

Parent absolute value function:

`f(x)=|x|`

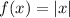
Graph of the parent absolute value function:

• Line |y| = -x where x ≤ 0
• Line |y| = x where x ≥ 0
• Vertex at (0, 0)

Therefore:

• The domain of the parent function is unrestricted: {-∞, ∞)
• The range of the parent function is restricted: [0, ∞)

If function f(x) is reflected across the y-axis:

`\implies f(-x)=|-x|`

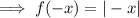
The reflection does not change the graph as the parent function is symmetric about the y-axis.

If function f(x) is translated to the left 5 units:

`\implies f(x+4)=|x+4|`

The domain remains unrestricted and the range remains [0, ∞).

Therefore, both the domain and range of the transformed function are the same as those of the parent function.