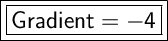Answer:
Gradient = -4
Explanation:
The gradient of a line (often referred to as its "slope") represents the rate of change of the line's vertical position (y-coordinate) with respect to its horizontal position (x-coordinate).
To find the gradient of a line segment between two points, we can substitute the two points into the gradient formula.
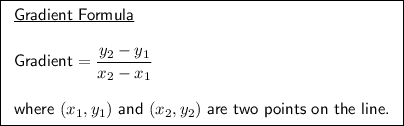
Given endpoints of the line segment:
Substitute the points into the gradient formula:
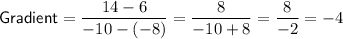
Therefore, the gradient of the line segment between the points (-8, 6) and (-10, 14) is: