Explanation:
For Part A:
Refer to the photo for an explanation on how to graph z=x+y+24 and how to set up the first integral. I will not explain how to do the other five but I have placed them beneath....
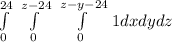
Where limits are,
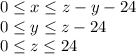
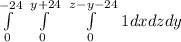
Where limits are,
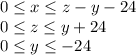
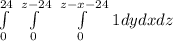
Where limits are,
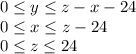
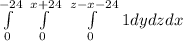
Where limits are,
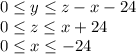
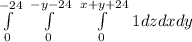
Where limits are,
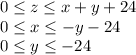
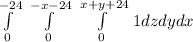
Where Limits are,
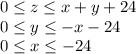
For Part B:
All the above limits equal the same volume. So I will just solve for one of the limits.
Evaluate,
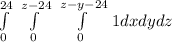
![\int\limits^(24)_0 {} \,\int\limits^(z-24)_0 {} \, (x]^(z-y-24) _0){} dydz \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/rp50hm3o42eqpl65z4mz75bcyo7bnscxrp.png)
![\int\limits^(24)_0 {} \,\int\limits^(z-24)_0 {} \, [(z-y-24)-0]{} dydz \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/3jy3dwrme9hxwhm77qef01ym733svbt5vm.png)
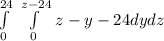
![\int\limits^(24)_0 {} \,[0-(y^(2) )/(2) -0]{} dz \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/snio3vjaqhvor85bk566kvfd2o69lrae65.png)
![\int\limits^(24)_0 {} \,(y^(2) )/(2) ]^(z-24) _(0) {} dz \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/7v8w7xv6lewafgkhqajka8n6rjbh6b8szx.png)
![\int\limits^(24)_0 {} \,[(((z-24)^(2))/(2))-0] {} dz \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/72u7vadywp23cqbyg8icks9ge7pmd70zfs.png)
![\int\limits^(24)_0 {} \,[(z^2)/(2)-288] {} dz \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/ahqr74qynfhg0pqlm5r95uif75vfsksr9h.png)
![[(z^3)/(6)-288z]^(24) _(0) {} \\\\](https://img.qammunity.org/2023/formulas/mathematics/college/ugrbe7gaer6ids5yj2sflh05t2jjxvgv17.png)
![[((24^3)/(6)-288(24))-0] {}](https://img.qammunity.org/2023/formulas/mathematics/college/m26953e4wl41j0ntepmb5l9zt338qeer1e.png)
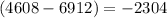
Answer: -2304