Answer:
1954
Explanation:
If a continuous random variable X is normally distributed with mean μ and variance σ²:
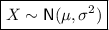
Given:
- mean μ = 4 oz
- standard deviation σ = 0.5 oz
First find the probability that the weight of an orange is less than 5 oz.
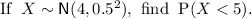
Method 1
Using a calculator:
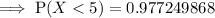
Method 2
Converting to the z-distribution.
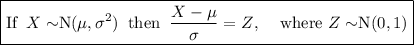
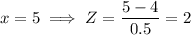
Using the z-tables for the probability:
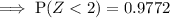
To find the expected number of oranges that will weigh less than 5 oz from a batch of 2000, multiply the total number of oranges by the probability calculated:
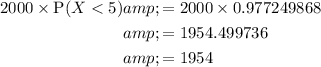
Therefore, 1954 oranges would be expected to weigh less than 5 oz.