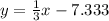Question

What is the equation of a line that is perpendicular to y = -3 and passes through the point (4,-6)

Answer 1

As always when trying to find the equation of a line, start with slope, as we will be working in slope-intercept form. The key word here is "perpendicular." Perpendicular lines always have Opposite Reciprocal slopes. An opposite reciprocal is the negative of the reciprocal of the ratio, or in simpler terms, a flipped fraction with a flipped sign.

`-3=-\frac31\\m=(-1)-\frac13\\m=\frac13`

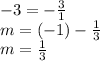
So, our equation so far is:

`y=\frac13x+b`

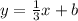
How do we solve for b? This lies in the given coordinates. To find the y-intercept given slope, you also need to be given any other coordinate pair that lies on the line. Here, we are given (4, -6). This means that for this pair of this line, x = 4 and y = -6. This means we can solve for the missing value. Let's put it in algebraic form.

`y=\frac13x+b\\-6=\frac134+b\\-6=1\frac13+b\\-6-1\frac13=1\frac13-1\frac13+b\\b=-7.333`

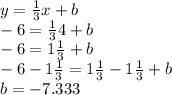
So, our function is:

`y = \frac13x-7.333`