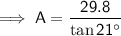Question

Two teenagers are standing on a 28-meter-high walking bridge and see a boat coming down the river toward the bridge. The angle of depression formed by the

teenagers' horizontal line of sight and their line of sight to the front of the boat is 21°. If the teenagers' horizontal line of sight is 1.8 meters above the bridge, how far away from the bridge is the front of the boat? Round your answer to the nearest tenth.

Answer 1

77.6 m

Explanation:

Angle of Depression

If a person stands at a point and looks down at an object, the angle between their horizontal line of sight and the object is called the angle of depression.

To find how far the bridge is from the front of the boat, model as a right triangle and solve using the tan trigonometric ratio.

Tan trigonometric ratio

`\sf \tan(\theta)=(O)/(A)`

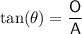
where:

• θ is the angle.
• O is the side opposite the angle.
• A is the side adjacent the angle.

Given information:

• Height of bridge = 28 m
• Person height = 1.8 m
• Angle of depression = 21°

As the teenagers' line of sight is 1.8 m above the bridge, the side of the right triangle opposite the angle of depression is:

• 28 + 1.8 = 29.8 m

Therefore:

`\implies \sf \tan21^(\circ)=(29.8)/(A)`

`\implies \sf A=(29.8)/(\tan21^(\circ))`

`\implies \sf A=77.6\;m\;\;(nearest\;tenth)`