Question

Answer the attached questions

Answer 1

Explanation:

89,83,91,92,93,x

n=6

average=91

total=91*6=546

89+83+91+92+93+x=546

448+x=546

x=546-448=98

Answer 2

Explanation:

1)

Let Andre's grade needs to be a x on his next test

Hence,

`\displaystyle\\(89+83+91+92+93+x)/(6) =91\\\\(448+x)/(6) =91`

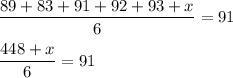
Multiply both parts of the equation by 6:

`448+x=91(6)\\\\448+x=546\\\\448+x-448=546-448\\\\x=98`

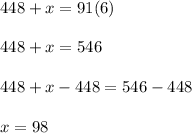
2)

`\displaystyle\\(1000+1181+1191+1200+1268+1328+2584+x)/(8) =1344\\\\(9752+x)/(8)=1344`

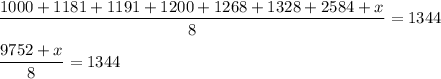
Multiply both parts of the equation by 8:

9752+x=1344(8)

9752+x=10752

9752+x-9752=10752-9752

x=$1000

3)

302, 293, 218, 330, 199, 253, 288

Arrange this series:

199, 218, 253, 288, 293, 302, 330

`\displaystyle\\a)\ the \ median = \$288\\\\b) \ the\ mean =(199+218+253+288+293+302+330)/(7) \\\\=(1883)/(7) \\\\=\$269\\c)\\\\(1883+x)/(8) =269+5\\\\(1883+x)/(8) =274`

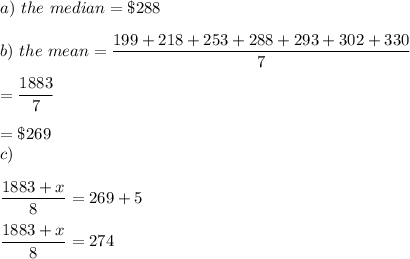
Multiply both parts of the equation by 8:

1883+x=274(8)

1883+x=2192

1883+x-1883=2192-1883

x=$309