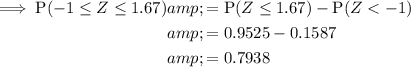Answer:
0.7938
Explanation:
The given graph is a normal distribution curve.
If a continuous random variable X is normally distributed with mean μ and variance σ²:
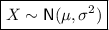
Given:
- mean μ = 100
- standard deviation σ = 15
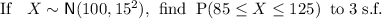
Therefore, we need to find the area to the left of x = 125 and subtract the area to the left of x = 85.
Method 1
Using a calculator:
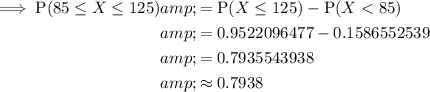
Method 2
Converting to the z-distribution.
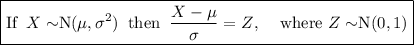
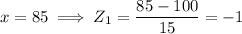

Using the z-tables to find the corresponding probabilities (see attachments).