Question

Ezra is occasionally asked to work the check-out line during his shifts at the Hy-Vee grocery store. During a recent lesson on Newton's

Laws, he re-lived a memory from work. He wrote the following Physics problem and he wants you to solve it.
The handle of a paper grocery sack has a breaking strength of 298 N. Ezra loads the bag with 18.8-kg of soup cans. With what
maximum acceleration can he lift the sack upward without breaking the handles?

Answer 1

Acceleration = 6.05 m/s²

Step-by-step explanation:

Fmax = 298 N

m = 18.8 kg

g = 9.8 m/s²

___________

a - ?

According to Newton's 2nd law:

Fmax = m·(g + a)

g + a = Fmax / m

Acceleration:

a = Fmax / m - g

a = 298 / 18.8 - 9.8 ≈ 6.05 m/s²

Answer 2

Approximately
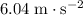`6.04\; {\rm m\cdot s^(-2)}`, assuming that
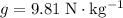`g = 9.81\; {\rm N \cdot kg^(-1)}` and that the mass of the bag is negligible.

Step-by-step explanation:

There are two forces on the paper bag:

• Upward tension in the handle,
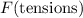  `F(\text{tensions})`, and
• Downward weight of the bag and its contents,
  `F(\text{weight})`.

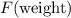It is given that the tension in the handle
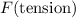`F(\text{tension})` should not exceed
`298\; {\rm N}`.

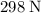Let
`g` denote the gravitational field strength. The mass of the bag and its contents is
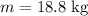`m = 18.8\; {\rm kg}`. Their weight will be
`F(\text{weight})= m\, g`.

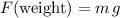SInce
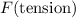`F(\text{tension})` and
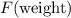`F(\text{weight})` are in opposite directions, the resultant force on the bag will be:

`F(\text{net}) = F(\text{tension}) - F(\text{weight})`.

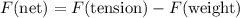Divide the net force by mass to find the acceleration
`a` of the bag:

`\begin{aligned}a &= \frac{F(\text{net})}{m} \\ &= \frac{F(\text{tension}) - F(\text{weight})}{m} \\ &= \frac{F(\text{tension}) - m\, g}{m} \\ &= \frac{F(\text{tension})}{m} - g\end{aligned}`.

Since
`F(\text{tension}) \le 298\; {\rm N}`:

`\begin{aligned} a &= \frac{F(\text{tension})}{m} - g \\ &\le \frac{298\; {\rm N}}{18.8\; {\rm kg}} - 9.81\; {\rm N \cdot kg^(-1)} \\ &\approx 6.04\; {\rm N \cdot kg^(-1)} \\ &=6.04\; {\rm m\cdot s^(-2)}\end{aligned}`.

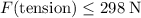Note the unit conversion:
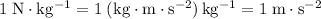`1\; {\rm N \cdot kg^(-1)} = 1\; {\rm (kg \cdot m\cdot s^(-2))\, kg^(-1)} = 1\; {\rm m\cdot s^(-2)}`.