Question

Why is there no maximum multiple and minimum divisor?​

Answer 1

Theme: LCM & GCM

`\textbf{Problem :}`

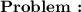
Why there is no greatest common multiple and least common divisor.

RESOLUTION :-

Before understanding why there is no greatest common multiple, let's see with an example what a common multiple of two numbers means.

Let the multiples of the numbers 18 and 24 be denoted by

`\sf{A \: \: } and\textrm{ \sf B respectively}`

`\textrm{ \sf A} = \{ \sf 18\ ;\ 36\ ;\ 54\ ;\ \boldsymbol{72}\ ;\ 90\ ;\ 108\ ;\ 126\ ;\ \boldsymbol{144}\ ;\ 162\ ;\ 180\ ;\ 198\ ;\ \boldsymbol{216} \ldots \}`

`\textrm{ \sf B} = \{ \sf 24\ ;\ 48\ ;\ \boldsymbol{72}\ ;\ 96\ ;\ 120\ ;\ \boldsymbol{144}\ ;\ 168\ ;\ 192\ ;\ \boldsymbol {216} \ldots \}`

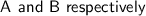
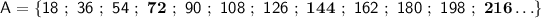
The highlighted numbers are the common multiples of 18 and 24, they are called common because these numbers are found in both sets. Note that there is an infinite and increasing number of common multiples for two numbers, for this reason it is meaningless to talk about a greatest common multiple, because there is no maximum. On the other hand, we can talk about a minimum and in this example the least common multiple is 72.

The common divisors of both numbers are highlighted. Let's see another example.

Let's note that for both cases the
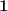`\boldsymbol{1}`is repeated and it will always be so for any set of numbers we choose, since the unit is a divisor of any positive integer number, in case we want to mention the least common divisor of a set of positive integers, the answer will always be the unit, since the unit is the smallest positive integer and since it is always present this is the minimum.

As can be seen, it is trivial to talk about the least common divisor, but it is interesting to talk about the greatest common divisor since it varies according to the set of numbers chosen.

`\sf RESPONSE :-`

¡Bye!