Answer:
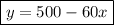
where:
- x is the time (in hours).
- y is the car's distance from Austin (in miles).
Explanation:
Define the variables:
- Let x be the time (in hours).
- Let y be the car's distance from Austin (in miles).
Given:
- When x = 0, y = 500.
- When x = 5, y = 200.
Find the rate of change:

Therefore, for every hour that passes, the car is 60 miles closer to Austin.
Therefore, the function that describes the car's distance from Austin is:
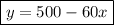
where:
- x is the time (in hours).
- y is the car's distance from Austin (in miles).