Question

An object is projected with a speed of 30m/s in a direction that makes an angle of 30° with the ground level . Cal. the length of time the object takes to reach the highest point of it's flight​

Pls help tommorow is the deadline else I'll loose my marks
thanks

Answer 1

1.53 seconds (2 d.p.)

Step-by-step explanation:

When a body is projected through the air with initial speed u, at an angle of θ to the horizontal, it will move along a curved path.

Therefore, trigonometry can be used to resolve the body's initial velocity into its vertical and horizontal components:

• Horizontal component of u (x) = u cos θ
• Vertical component of u (y) = u sin θ

Because the projectile is modeled as moving only under the influence of gravity, the only acceleration the projectile will experience will be acceleration due to gravity (a = 9.8 m/s²).

Constant Acceleration Equations (SUVAT)

`\boxed{\begin{array}{c}\begin{aligned}v&=u+at\\\\s&=ut+(1)/(2)at^2\\\\ s&=\left((u+v)/(2)\right)t\\\\v^2&=u^2+2as\\\\s&=vt-(1)/(2)at^2\end{aligned}\end{array}} \quad \boxed{\begin{minipage}{4.6 cm}$s$ = displacement in m\\\\$u$ = initial velocity in ms$^(-1)$\\\\$v$ = final velocity in ms$^(-1)$\\\\$a$ = acceleration in ms$^(-2)$\\\\$t$ = time in s (seconds)\end{minipage}}`

When using SUVAT, assume the object is modeled as a particle and that acceleration is constant.

If an object is thrown at 30 m/s from flat ground at an angle of 30° then:

• Horizontal component of u = 30 cos 30°
• Vertical component of u = 30 sin 30°

When the object reaches its maximum height, the vertical component of its velocity will momentarily be zero.

Resolving vertically, taking up as positive:

• 
  `u = 30 \sin 30^(\circ), \quad v = 0, \quad a = -9.8`

`\begin{aligned}\textsf{Using}\;\; v &=u+at:\\\\\implies 0 &=30 \sin 30^(\circ)+(-9.8)t\\0 &=15-9.8t\\9.8t &=15\\t &=(15)/(9.8)\\t&=1.53\;\; \sf s\;(2 \; d.p.)\end{aligned}`

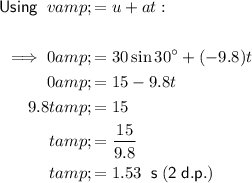
Therefore, the length of time the object takes to reach the highest point of its flight is 1.53 seconds (2 d.p.).