Question

NEED ASAP

A rectangular solid has width , a length of 7 more than the width, and a height that is equivalent to 15 decreased by 3 times the width. Express the volume in terms of the wic
Then find the maximum volume to the nearest whole number cubic unit.

Answer 1

⇒ Let the width of the the rectangular solid be x since it was not given as a value meaning W=x

⇒It is given that the length is 7 more than the width meaning the length exceeds the width by 7 , L=x+7

⇒The height is 15 decreased by 3 times the size of the width which can be written as H=15 -3(x)

..The formula to calculate the volume of the rectangular solid is given by V=L×W×H

where the Length is (x+7)

where the Width is (x)

where the Height is 15-3x

Volume in terms of width is :

______________________________________________________

V=(x+7)×(x)×(15-3x)

`V=(x^(2) +7x)(15-3x)\\V=15x^(2) -3x^(3) +105x-21x\\V=- 3x^(3)+ 15x^(2) +84x`

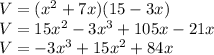
⇒to find the maximum volume you derivate V and equate the derivative to 0 then solve for x

⇒ Derivating we get

`V'(x)=-27x^(2) +30x+84x\\`

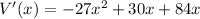
⇒For the maximum volume let V'(x)=0 and solve for x ,Note in this step where you are solving for x you are getting the x-value where V is maximum, to get the volume itself we will plug in the value of x we found in the original equation and simplify to get V

`0=-27x^(2) +30x+84\\-27x^(2) +30x+84=0\\-3(9x^(2) -10x-28)=0\\\\(-3(9x^(2) -10x-28))/(-3) =(0)/(-3) \\9x^(2) -10x-28=0\\x=\frac{-b+/-\sqrt{b^(2)-4ac } }{2a} \\x=\frac{-9+/-\sqrt{(9)^(2) -4(9)(-28)} }{2(18)}`

Note since this is a quadratic equation we will have two solutions.

if we simplify further using a calculator we get x= -1.217006237 and 2.328117348

Let us find the maximum volume by plugging the values we got for x .

`when \\x=-1.217006237\\V=-3(-1.217006237)^(3) +15(-1.217006237)^(2) +84(-1.217006237)\\V=-74.60442212`

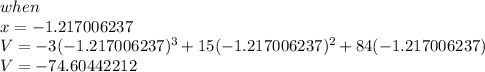
⇒Note this solution cannot be applied since Volume will never be negative.!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!Please keep that in mind

______________________________________________________

`when\\x=2.328117348\\V=-3(2.328117348)^(3) +15(2.328117348)^(2) +84(2.328117348)\\V=239.00777143`

⇒The solution is applicable The Maximum volume of the reactangular solid is ≅239.008