Question

Can you please help with problem 23

Answer 1

#22

• Find the height using the trigonometric ratio.
• Trigonometric ratio used here is:

`\boxed{\mathfrak{\sin( \theta)=(perpendicular)/(hypotenuse)}}`

• θ = 45°
• Perpendicular = ?
• Hypotenuse = 22

`\tt \: \sin(45 \degree) = (p)/(22)`

`\tt \: ( √(2) )/(2) = (p)/(22)`

`\tt \: 22 √(2) = 2p`

`\tt11 √(2) = p \: or \: p = 11 √(2)`

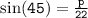
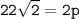
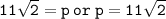
➪Therefore th value of perpendicular is 15.5 when rounded off...

#23

• Now, We will find the area with the help of height that we just found using the trigonometric ratio.
• The formula to find area of parallelogram is:

`\boxed{ \mathfrak{area = base * height}}`

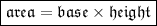
• Base = 26 in. [Since opposite sides of parallelogram are equal and parallel]
• Height = 15.5 in.

`\sf \: area = 26 * 15.5 \\ \sf \: area = 403 \: {in}^(2)`

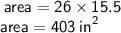
➪Thus, The area of parallelogram is 403 inch²...~

Answer 2

`\\ \rm\longmapsto sin45=(h)/(22)`

`\\ \rm\longmapsto h=22sin45=22(0.71)=15.6in`

• Parallel sides of a parallelogram are equal.

`\\ \rm\longmapsto Area`

`\\ \rm\longmapsto Base(Height)`

`\\ \rm\longmapsto 26(15.6)=405.6in^2`