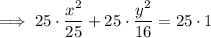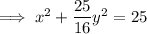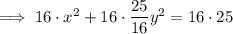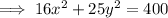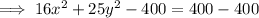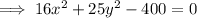Question

Write the equation in standard form for the conic section described below.

The sum of the distance of any point (x,y) in this conic to the two focuses F1=(-3,0) and F2=(3,0) is constant and equal to 10

Answer 1

`16x^2+25y^2-400=0`

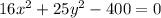
Explanation:

Given:

• The sum of the distance of any point (x, y) in this conic to the two focuses F₁=(-3,0) and F₂=(3, 0) is constant and equal to 10.

There are 4 types of conic sections:

1. Circles (one focus).
2. Parabolas (one focus).
3. Ellipses (two foci).
4. Hyperbolas (two foci).

The definition of an ellipse is:

• The set of points in a plane such that the sum of the distance from a point to each focus is constant.

Therefore, the given definition is one for an ellipse.

`\boxed{\begin{minipage}{7.4 cm}\underline{General equation of an ellipse}\\\\$((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center. \\ \phantom{ww}$\bullet$ $(h\pm a,k)$ or $(h,k\pm b)$ are the vertices. \\ \phantom{ww}$\bullet$ $(h\pm c,k)$ or $(h,k\pm c)$ where $c^2=a^2-b^2$.\\\end{minipage}}`

As the given foci are (-3, 0) and (3, 0), they are on the x-axis. Therefore:

• h = 0
• k = 0
• c = 3

Therefore, the major axis is on the x-axis and the vertices are (h±a, k) and the co-vertices are (h, k±b).

The constant is the major axis which is 2a. Given the constant is 10:

`\implies 2a=10`

`\implies a=5`

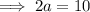
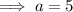
Since c² = a² - b²:

`\implies 3^2=5^2-b^2`

`\implies b^2=5^2-3^2`

`\implies b^2=25-9`

`\implies b^2=16`

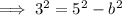
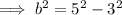
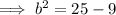
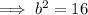
Therefore, the equation for the conic section (ellipse) is:

`\implies ((x-0)^2)/(5^2)+((y-0)^2)/(16)=1`

`\implies (x^2)/(25)+(y^2)/(16)=1`

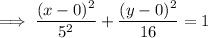
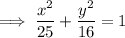
In standard form:

`\implies 25 \cdot (x^2)/(25)+25 \cdot (y^2)/(16)=25 \cdot 1`

`\implies x^2+(25)/(16)y^2=25`

`\implies 16 \cdot x^2+16 \cdot (25)/(16)y^2=16 \cdot 25`

`\implies 16x^2+25y^2=400`

`\implies 16x^2+25y^2-400=400-400`

`\implies 16x^2+25y^2-400=0`