Question

X^4+19x^2-20=0 please

Answer 1

x = 1, -1

Explanation:

Let u = x², therefore:

`\displaystyle{ {u}^(2) + 19u - 20 = 0}`

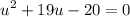
Find two numbers that has product of -20 and sum of 19, and those numbers are 20 and -1

`\displaystyle{(u + 20)(u - 1) = 0}`

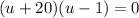
Therefore:

`\displaystyle{u = - 20,1}`

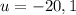
Switch back to x²

`\displaystyle{ {x}^(2) = - 20,1}`

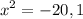
But x² = -20 has no real solutions so we are left with

`\displaystyle{ {x}^(2) = 1}`

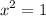
Square root both sides

`\displaystyle{ \sqrt{ {x}^(2) } = √(1)}`

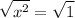
Cancel square and square root then write plus-minus

`\displaystyle{ x = \pm \sqrt 1} \\ \\ \displaystyle{ x = \pm 1}`

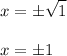
Therefore x = 1, -1