Question

Solve the equation secθtanθ = 1 for 0<θ<2pi

Answer 1

`sec(\theta )tan(\theta )=1\implies \cfrac{1}{cos(\theta)}\cdot \cfrac{sin(\theta)}{cos(\theta)}=1\implies \cfrac{sin(\theta)}{cos^2(\theta)}=1 \\\\\\ sin(\theta)=cos^2(\theta)\implies sin(\theta)=1-sin^2(\theta) \implies sin^2(\theta)+sin(\theta)-1=0`

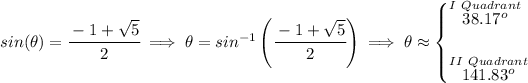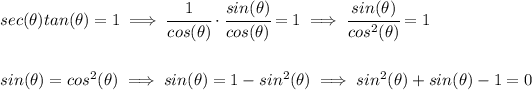
well, it doesn't quite factor into neat integers, so let's plug it in the quadratic formula

`~~~~~~~~~~~~\textit{quadratic formula} \\\\ \stackrel{\stackrel{a}{\downarrow }}{1}sin^2(\theta)\stackrel{\stackrel{b}{\downarrow }}{+1}sin(\theta)\stackrel{\stackrel{c}{\downarrow }}{-1}=0 \qquad \qquad sin(\theta)= \cfrac{ - b \pm \sqrt { b^2 -4 a c}}{2 a}`

`sin(\theta)= \cfrac{ - (1) \pm \sqrt { (1)^2 -4(1)(-1)}}{2(1)} \implies sin(\theta) = \cfrac{ -1 \pm \sqrt { 1 +4}}{ 2 } \\\\\\ sin(\theta)= \cfrac{ -1 \pm \sqrt { 5 }}{ 2 }\implies sin(\theta)= \begin{cases} \frac{ -1 - \sqrt { 5 }}{ 2 } ~~ \bigotimes\\\\ \frac{ -1 + \sqrt { 5 }}{ 2 } ~~ \checkmark \end{cases}`

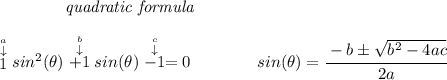
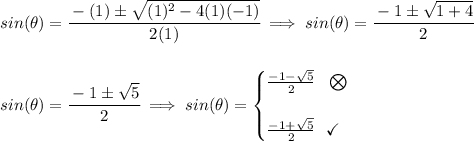
now, why is the 1st value not valid? well, the 1st value gives us a value that's over -1, about -1.62, and the sine function is always -1 ⩽ sine ⩽ 1, so we can't use that, so let's use the 2nd value which is within range

`sin(\theta)=\cfrac{ -1 + \sqrt { 5 }}{ 2 }\implies \theta =sin^(-1)\left( \cfrac{ -1 + \sqrt { 5 }}{ 2 } \right)\implies \theta \approx \begin{cases} \stackrel{I~Quadrant}{38.17^o}\\\\ \stackrel{II~Quadrant}{141.83^o} \end{cases}`