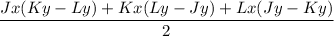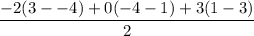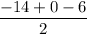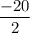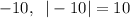Answer: 10 units²
Explanation:
To find the area of a triangle when given its vertices, we can use this formula:
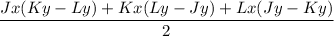
We will plug in our coordinate points and solve. The area will be the absolute value simplification of this expression.
J(-2, 1) is (Jx, Jy), K(0, 3) is (Kx, Ky), and L(3,-4) is (Lx, Ly).