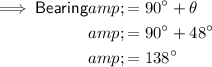Answer:
138° (nearest degree)
Explanation:
Bearing: The angle (in degrees) measured clockwise from north.
The given scenario can be modelled as a right triangle (see attachment).
Therefore, the bearing is 90° + θ (shown in green on the attached diagram).
To find angle θ, use the cosine trigonometric ratio:

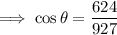
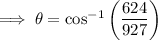
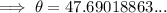
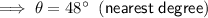
Therefore, the bearing of the drawbridge from the tower is: