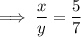Answer:
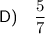
Explanation:
Given equations:
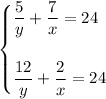
Rearrange the first equation to eliminate the fractions:
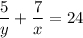
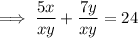

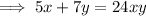
Rearrange the second equation to eliminate the fractions:
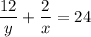
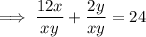
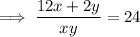

Substitute the first equation into the second equation:
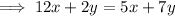
Rearrange so that x is on the left side and y is on the right side:
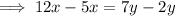
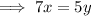
Therefore, the ratio of x to y is: