Question

A racket exerted an average force of 152N on a ball initially at rest. If the ball has a mass of 0.07kg and was in contact with the racket for 0.03s, what was the kinetic energy of the ball as it left the racket?

Answer 1

Approximately
`150\; {\rm J}` (
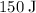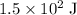`1.5* 10^(2)\; {\rm J}`) assuming that no other force is acting on the ball.

Step-by-step explanation:

The net impulse on an object will be equal to the change in the momentum.

Under the assumptions, the force from the racket is the only force on the ball. Since this net force is constant, multiplying this force
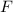`F` by the duration
`t` of contact will give the value of the impulse:

`\begin{aligned} J &= t\, F \\ &= (0.03\; {\rm s})\, (152\; {\rm N}) \\ &= 4.56\; {\rm kg\cdot m \cdot s} \end{aligned}`.

Note the unit conversion:
`1\; {\rm N \cdot s} = 1\; {\rm (kg \cdot m\cdot s^(-2))\cdot s} = 1\; {\rm kg \cdot m\cdot s^(-1)}`.

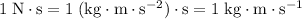If an object of mass
`m` is travelling at a velocity of
`v`, the momentum of that object will be
`p = m\, v`.

The momentum of the ball was initially
`0\; {\rm kg \cdot m\cdot s^(-1)}` since the ball was initially at rest. Hence, the net impulse of
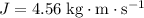`J =4.56\; {\rm kg \cdot m\cdot s^(-1)}` will increase the momentum of this ball to
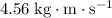`4.56\; {\rm kg \cdot m\cdot s^(-1)}`. Divide the momentum of the ball by mass to find the velocity of the ball:

`\begin{aligned}v &= (p)/(m) \\ &= \frac{4.56\; {\rm kg \cdot m\cdot s^(-1)}}{0.07\; {\rm kg}} \\ &\approx 65.1\; {\rm m\cdot s^(-1)}\end{aligned}`.

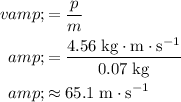If an object of mass
`m` is travelling at a speed of
`v`, the kinetic energy of that object will be
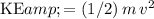`\text{KE} &= (1/2)\, m\, v^(2)`. Since this ball of mass
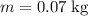`m = 0.07\; {\rm kg}` is travelling at
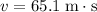`v = 65.1\; {\rm m\cdot s}`, the kinetic energy of this ball will be:

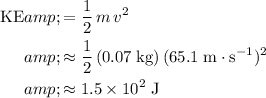`\begin{aligned}\text{KE} &= (1)/(2)\, m\, v^(2) \\ &\approx (1)/(2)\, (0.07\; {\rm kg})\, (65.1\; {\rm m\cdot s^(-1)})^(2) \\ &\approx 1.5* 10^(2)\; {\rm J}\end{aligned}`.