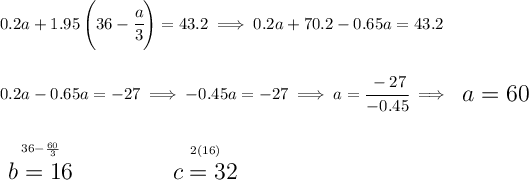a = solution at 20% acid
b = solution at 35% acid
c = solution at 80% acid
now, we know she wants to use two times as much of "c" as there's of "b", which is a mumble jumble for saying whatever "b" is, well "c" is twice that much, namely c = 2b. We also know the whole mixture will be 108 liters of 40% acid.
let's convert those percentages to decimals and let's see how much all those liters are
![\begin{array}{lcccl} &\stackrel{liters}{quantity}&\stackrel{\textit{\% of }}{amount}&\stackrel{\textit{liters of }}{amount}\\ \cline{2-4}&\\ \textit{20\% sol'n}&a&0.20&0.2a\\ \textit{35\% sol'n}&b&0.35&0.35b\\ \boxed{\textit{80\% sol'n}}&c&0.80&0.8c\\ \textit{80\% sol'n}&2b&0.80&1.6b\\ \cline{2-4}&\\ mixture&108&0.40&43.2 \end{array}~\hfill \begin{cases} a+b+\stackrel{c}{2b}=108\\\\ 0.2a+0.35b+1.6b=43.2 \end{cases} \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2023/formulas/mathematics/high-school/eo8r2raa66p9elaw1nj51gutuy74723fub.png)