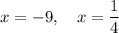Answer:
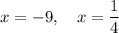
Explanation:
Given function:
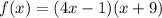
The roots of a function are the x-values for which the function equals zero. Therefore, to find the roots, set the function to zero and solve for x.
Set the function to zero:
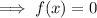
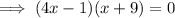
Zero Product Property
If a ⋅ b = 0 then either a = 0 or b = 0 (or both).
Apply the zero product property:
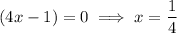
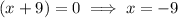
Therefore, the roots of the given function are: