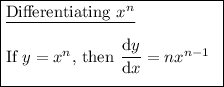Question

The radius r of a circle is increasing at a rate of 4 centimeters per minute.

- Find the rates of change in the area

when r = 37 centimeters.


- The length s of each side of an equilateral triangle is

increasing at a rate of 13 feet per hour. Find the rate of change

of the area when s = 41 feet.

Answer 1

929.91 cm²/min

461.59 ft²/min

Explanation:

`\boxed{\begin{minipage}{4cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \end{minipage}}`

Differentiate the expression for area with respect to r:

`\implies \frac{\text{d}A}{\text{d}r}=2\pi r`

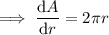
Given the radius is increasing at a rate of 4 centimeters per minute:

• 
  `\frac{\text{d}r}{\text{d}t}=4`

Use the chain rule to find an expression for the rate of change in the area with respect to time:

`\implies \frac{\text{d}A}{\text{d}t}=\frac{\text{d}A}{\text{d}r} * \frac{\text{d}r}{\text{d}t}`

`\implies \frac{\text{d}A}{\text{d}t}=2 \pi r * 4`

`\implies \frac{\text{d}A}{\text{d}t}=8 \pi r`

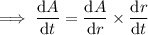
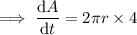
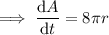
When r = 37 cm:

`\implies \frac{\text{d}A}{\text{d}t}=8\pi (37)`

`\implies \frac{\text{d}A}{\text{d}t}=296 \pi`

`\implies \frac{\text{d}A}{\text{d}t}=929.91\; \sf (2\;d.p.)`

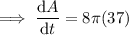
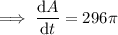
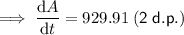
Therefore, the rate of change in the area when the radius is 37 centimeters is 929.91 cm²/min.

--------------------------------------------------------------------------------------

`\boxed{\begin{minipage}{5 cm}\underline{Area of an equilateral triangle}\\\\$A=(√(3))/(4)s^2$\\\\where:\\ \phantom{ww}$\bullet$ $s$ is the side length. \\ \end{minipage}}`

Differentiate the expression for area with respect to s:

`\implies \frac{\text{d}A}{\text{d}s}=(2√(3))/(4)s=(√(3))/(2)s`

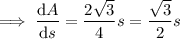
Given the length of each side is increasing at a rate of 13 feet per hour.

`\implies \frac{\text{d}s}{\text{d}t}=13`

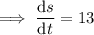
Use the chain rule to find an expression for the rate of change of the area with respect to time:

`\implies \frac{\text{d}A}{\text{d}t}=\frac{\text{d}A}{\text{d}s} * \frac{\text{d}s}{\text{d}t}`

`\implies \frac{\text{d}A}{\text{d}t}=(√(3))/(2)s * 13`

`\implies \frac{\text{d}A}{\text{d}t}=(13√(3))/(2)s`

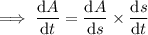
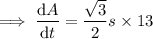
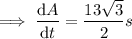
When s = 41 ft:

`\implies \frac{\text{d}A}{\text{d}t}=(13√(3))/(2)(41)`

`\implies \frac{\text{d}A}{\text{d}t}=(533√(3))/(2)`

`\implies \frac{\text{d}A}{\text{d}t}=461.59 \sf \;\;(2\;d.p.)`

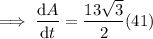
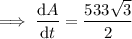
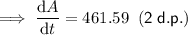
Therefore, the rate of change in the area when the side length is 41 feet is 461.59 ft²/min.

Differentiation rules used:

`\boxed{\begin{minipage}{4.5 cm}\underline{Differentiating $x^n$}\\\\If $y=x^n$, then $\frac{\text{d}y}{\text{d}x}=nx^(n-1)$\\\end{minipage}}`