Question

Find the compound interest on Rs. 48000 for one year at 8% per annum, when compounded half-yearly

Answer 1

Rs.3916.80

Explanation:

Compound Interest Formula

`\large \text{$ \sf I=P\left(1+(r)/(n)\right)^(nt)-P $}`

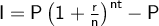
where:

• I = Interest.
• P = Principal amount.
• r = Interest rate (in decimal form).
• n = Number of times interest is applied per year.
• t = Time (in years).

Given values:

• P = Rs.48000
• r = 8% = 0.08
• n = 2 (half-yearly)
• t = 1

Substitute the given values into the formula and solve for I:

`\implies \sf I=48000\left(1+(0.08)/(2)\right)^(2 * 1)-48000`

`\implies \sf I=48000(1+0.04)^(2)-48000`

`\implies \sf I=48000(1.04)^(2)-48000`

`\implies \sf I=48000(1.0816)-48000`

`\implies \sf I=51916.8-48000`

`\implies \sf I=Rs.3916.80`

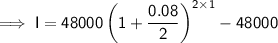
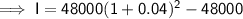
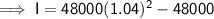
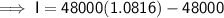
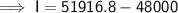
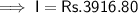
Therefore, the interest is Rs.3916.80.

Answer 2

• Rs. 3916.80

--------------------------------

Compound interest formula

• 
  `I=P[(1+r/n)^(nt)-1]`, where I-interest, P-principal, r-rate, t- time, n- number of compounds

Given

• P = Rs. 48000,
• r = 8% = 0.08,
• t = 1,
• n = 2.

Find the amount of interest

• 
  `I=48000[(1+0.08/2)^(2*1)-1]=48000(1.04^2-1)=3916.80`