Question

Find the Area of the figure below, composed of a rectangle with a semicircle

removed from it. Round to the nearest tenths place.

Answer 1

111.5

Explanation:

First have to find the area of the whole rectangle

1. using the formula, =length × width
2. area of the whole rectangle =12 ×14
3. area of the whole rectangle =168

After that, we find the area of the respective semicircle

1. using the formula,
2. 
   `\frac{pir {}^(2) }{2}`
3. where the diameter of the semicircle is 12, hence the radius will be 6
4. 
   `\frac{\pi(6) {}^(2) }{2}`
5. 56.55

Now we find the area of the rectangle without the semicircular portion by subtracting the area of the semicircle from that of the whole rectangle

1. hence, 168 -56.55
2. 111.5

Answer 2

Explanation:

12 *14 = 168

168 is the entire rectangle, now subtract the area of the semi-circle from that

The circle has a radius of 6, we know that b/c the width of the rectangle is 12 so half of that is 6

the circle is called a semi-circle so we know it's 1/2 of a circle and that it fits perfectly in the 12 size of the rectangle

this just confirms that the radius of the circle is 6

area of a circle is
`\pi`
`r^(2)`

`\pi`*
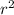
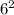`6^(2)` = 113.0973

but that's the size of the entire circle, so divide that in 2 to get half the circle

113.0973 / 2 = 56.5487

now subtract that from our entire rectangle

168-56.5487 = 111.4513

round that to the nearest 10th

111.5