Answer: No Solutions
The system is inconsistent.
======================================================
Step-by-step explanation:
A+2 = B is the same as B = A+2
We can replace B with A+2 in the first equation and solve for "A" like shown below.
A-B = 2
A-( B ) = 2
A - (A+2) = 2
A-A-2 = 2
0A-2 = 2
0-2 = 2
-2 = 2
We run into a problem. The "A" variable cancels out and the left hand side does not match with the right hand side. We get a contradiction.
No matter what we pick for A and B, there aren't any solutions to this system. We consider this system inconsistent.
--------------------------------
Another approach:
Rearrange the terms of A+2 = B to get A-B = -2
The original system of

turns into
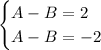
Now let C = A-B, so we can replace each "A-B" with C.
The system now updates to
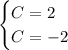
But it's impossible for a variable to take on more than one value at a time. C is not able to be equal to both 2 and -2 at the same time. This is another way to arrive at a contradiction which leads to "no solution".
--------------------------------
A third approach:
Replace each "A" with x. Replace each "B" with y
- A-B = 2 becomes x-y = 2 and solves to y = x-2
- A+2 = B becomes x+2 = y which is the same as y = x+2
If you were to graph those linear equations, then you should see parallel lines forming. Parallel lines never intersect. We would need them to intersect to form a solution (x,y). This is a visually quick way to see this system has no solutions.
Notice that y = x-2 and y = x+2 have the same slope m = 1, but different y intercepts.